| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- pcrnaseq
- single cell rna sequencing
- 통계학
- scanpy
- 티스토리챌린지
- endothelial
- np.trace
- bioinformatics
- 후기
- 주식투자
- Python
- 넘파이 매서드
- np.flatten
- np.diagflat
- 연구원
- 대학생주식
- journal meeting
- np.triu
- numpy
- liver
- Preprocessing
- Tutorial
- single cell rna sequening
- 대학원
- 선형대수
- scRNASeq
- 대학생재테크
- R
- 주식
- 오블완
- Today
- Total
biotechknowledge
[R을 활용한 통계학 개론]이항분포, 포아송분포, 정규분포 본문
1. 이항분포(Binomial Distribution)

이항분포는 고정된 시행 횟수 동안 특정 사건이 발생하는 횟수를 나타내는 이산 확률분포입니다.
이항분포의 n 과 k 에 따른 그래프 모양 변화, y 값은 그 값이 나올 확률을 의미한다.
1.1 정의
- 시행: 동일한 조건에서 여러 번 반복되는 실험(예: 동전 던지기).
- 결과: 두 가지 가능성(성공 또는 실패)이 존재.
- 성공 확률: 각 시행에서 성공할 확률은 일정하며 pp로 표시.
- 시행 횟수: n
1.2 예시
- 동전을 10번 던질 때 앞면이 6번 나올 확률.
- 공장에서 불량률이 5%5\%일 때, 20개 제품 중 불량품이 2개일 확률.
시행 횟수 n가 매우 크고, 성공 확률 p이 매우 작을 때 np -> m 이 되면 이항분포가 포아송 분포로 근사 가능하다. 예를들어, np=2 인경우 λ 인 포아송분포를 따른다. 공식 어차피 이해 못하고 번잡스럽기만 하니 일단 이렇게만 알아두자.
2. 포아송분포(Poisson Distribution)

포아송분포는 확률분포의 하나로, 일정 시간 또는 공간 내에서 어떤 사건이 발생하는 횟수를 모델링할 때 사용됩니다. 이는 주로 사건이 드물게 발생하는 상황을 설명하는 데 적합합니다.
포아송분포의 특징
- λ 값이 작을수록 분포는 왼쪽에 치우치고, λ값이 커질수록 대칭적이고 정규분포와 비슷해집니다.
- 모든 확률의 합은 항상 1이므로 막대들의 총 면적은 동일합니다.
포아송분포를 이용하여 추론하는 과정
- 문제 정의: 평균 발생 횟수() 추정 또는 사건 발생 확률 계산 목표 설정.
- 데이터 수집: 1시간 동안 콜센터 몇건의 전화를 받는지 확률을 구하고자 한다면, 10시간동안 각 1시간동안 몇 건의 전화가 오는지 조사하기. 일반적인 통계적 추론에서 표본 크기가 n >= 30 이면 중심극한정리에 의해 표본 평균이 안정적이라고 본다.
- 표본평균 계산: 평균내기
- 모델 적합성 검토: 데이터가 포아송분포를 따르는지 확인(포아송 분포에서 평균과 분산은 동일) ,-검정, KS-검정 등으로 데이터가 포아송분포에 적합한지 확인.
- 확률 계산: 추정된 으로 사건 발생 확률 계산. (포아송 분포 공식 사용)
- 결과 해석 및 의사결정: 계산된 확률에 기반한 판단.
- 검증 및 개선: 결과 검증, 추가 데이터 수집 및 모델 개선
단순히 포아송분포 뿐만 아니라 어떠한 종류의 분포든 위와같은 방식을 이용하여 모집단의 알고자하는 값(평균,분산)을 구해낸다.
2. 정규분포(Normal Distribution)

가우스 분포는 연속확률분포의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는 데에 자주 사용되며, 이것은 중심극한정리 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다. 평균이 0이고 표준편차가 1인 정규분포 N(0,1)를 표준정규분포 라고 한다.

동전을 10,30,50 번 던진다. 이 떄 나온 앞면의 수를 센다고 하자. 시행횟수를 늘릴수록 정규분포형태를 따른다.
과목이 다른 점수를 비교하기위해 표준화를 사용한다. 이때 표준화시키는 비교그룹은 동질하다고 가정한다.
모수(parameter)
모집단의 특성을 나타내는 값.
통계량(statistic)
표본들만의 함수로 표현. 즉, 통계량은 특정 모수를 추정하기 위해 표본을 이용하여 만든 함수
표본분포(sampling distribution)
통계량이 갖는 분포
임의표본(ramdom sample)
크기 n인 표본 X1,X2 ... Xn 이 동일한 분포(동일한 모집단)을 가지며, 서로 독립일때 X1,X2...Xn 을 임의표본이라 한다.
따름정리 : 모집단이 정규분포를 따른다면 표본평균의 분포가 정규분포를 따른다.
중심극한정리 : 모집단이 어떤 분포라도 n개 표본추출해서 표본평균을 구하면 정규분포를 따른다. (표본크기 > 25)


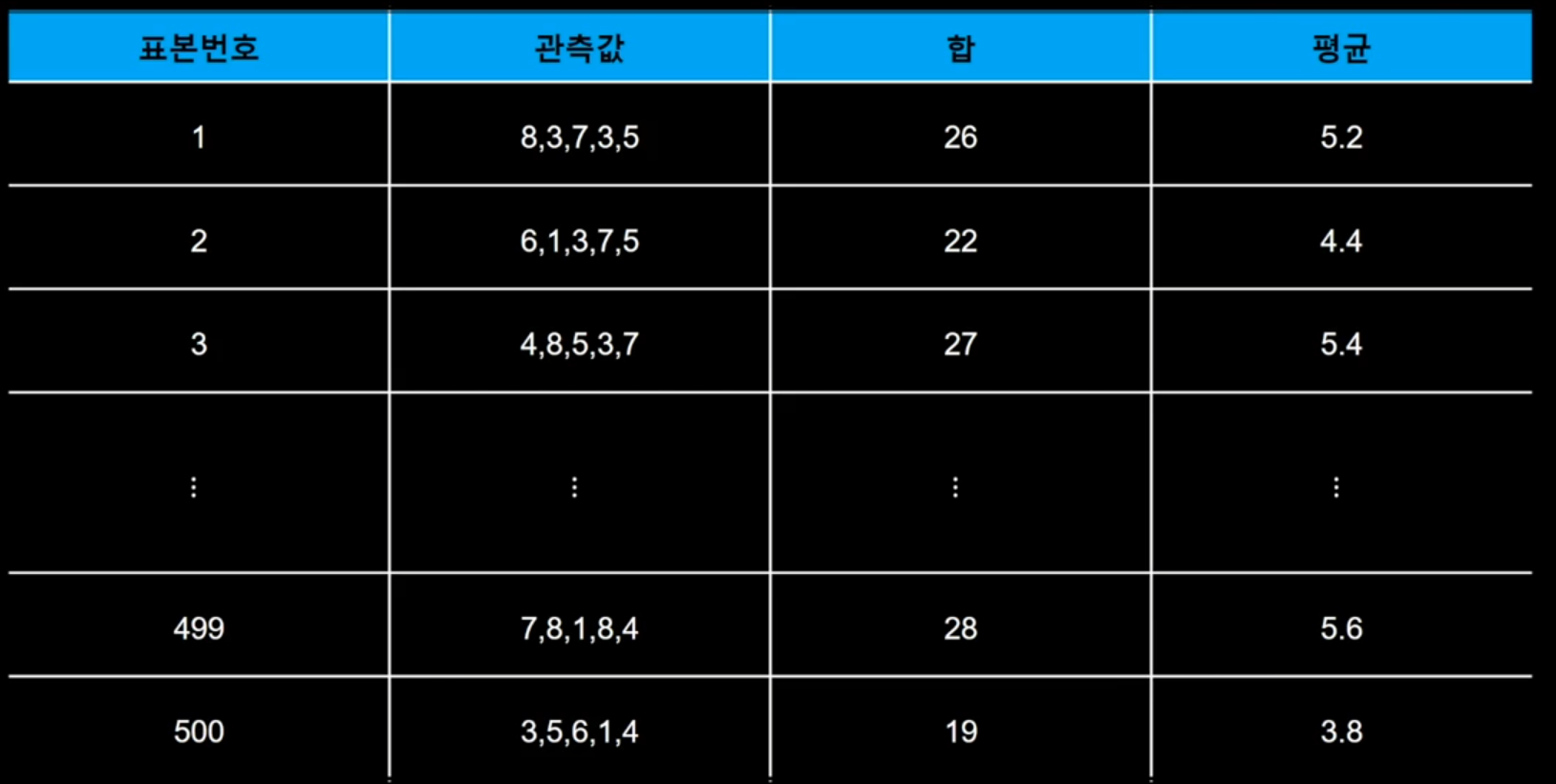
500개 샘플링: 표본평균은 모평균에 근사하고, 표본분산은 n수가 증가할수록 감소한다.

표본평균은 E(X) = 4.6, s.d(X) = 1.17 인 정규분포를 따른다.
'mathematics and statistics' 카테고리의 다른 글
| [R을 활용한 통계학 개론]확률변수, 확률분포, 확률밀도함수, 기대값 개념 설명 (1) | 2024.12.26 |
|---|---|
| [R을 활용한 통계한 개론]확률의 정의와 기본 개념, 조건부확률, 독립 (1) | 2024.12.10 |
| [R을 활용한 통계한 개론]중심, 퍼짐 측도, box plot, scatter plot, Correlation Coefficient 이해하기 (2) | 2024.11.23 |
| [R을 활용한 통계한 개론]통계학의 기본 개념 (모집단, 표본,자료의 종류) (1) | 2024.11.22 |
| [R을 활용한 통계한 개론]통계학이란 무엇인가? (1) | 2024.11.20 |




